An accurate method for determining the true azimuth of an ultra-short baseline

1 Introduction

In engineering surveying and mapping, the baseline direction is often expressed by Gaussian projection plane coordinate azimuth. In specific cases, the true azimuth of the baseline needs to be measured, such as geological and geophysical exploration, aviation, navigation, artillery shooting radar orientation, etc. The so-called true direction Angle, that is, a point to the North Pole of the direction line called true north line, also called the true meridian, from the point of the true north line, clockwise to the target direction line between the horizontal Angle, called the point of the true azimuth spoon. The method of determining the true azimuth of a baseline usually includes gyroscopic total station method and Gaussian projection correction method. It can be seen from the control measurement that the longer the distance between known points at both ends is, the more accurate the solution will be when solving the baseline coordinate azimuth; conversely, the shorter the side length is, the more difficult it is to accurately solve the coordinate azimuth. The same is true for solving the true azimuth. For example, when the aircraft inertial navigation system is calibrated and calibrated, its length is only tens of meters. It is extremely difficult to accurately calculate its true azimuth, because in the short distance,GNSS observation antenna phase center deviation, instrument calibration error, observation ephemeris and other factors have a great influence on its azimuth calculation. In the field of ultra-short baseline positioning, some scholars have done a lot of relevant research work. For example, Li Yu et al. compared and analyzed the processing accuracy of 24h data of PPE software with three baselines of different lengths. Wang Degang et al. analyzed the error source of ultra-short baseline positioning, namely; Yang Guihai et al. from ranging error, sounding error, improve the positioning accuracy of measuring equipment. There are many researches similar to the above, but the predecessors mainly discussed the accuracy of point position rather than the true azimuth Angle from the perspective of software testing or simulation technology. In addition, when the traditional Gaussian projection method is solving the true azimuth, it needs to project the geodetic coordinates to the Gaussian plane, and then calculate the coordinate azimuth, meridian convergence Angle and direction change to obtain the true azimuth. This process is complicated, easy to solve the deviation, and not strong in practicability.

In order to accurately and conveniently solve the ultra-short baseline true azimuth, based on the basic theory of station heart level coordinate system and combined with an aircraft inertial navigation test project, this study analyzed and discussed the practical application of station heart level coordinate system to solve the ultra-short baseline true azimuth in aircraft inertial navigation test. Compared with the traditional Gaussian projection correction method, the proposed method has no loss in accuracy and is convenient to solve.

The horizontal coordinate system of the model station takes the measuring station P as the origin, the normal line of point P as the Z axis, and the direction of the distance between the earth zenith as the positive direction. On the surface, the meridian direction is the X-axis, and the Y-axis is orthogonal to the X-axis and Z-axis. It is different from the origin of the coordinates of the two coordinate systems and the direction of the three coordinate axes of the space rectangular coordinate system, and there is a translation and rotation relationship. The station plane-of-heart coordinate system is generally used in deep space geodesy research. Since the true azimuth is to determine the azimuth from a single point to another point, this paper uses the definition of plane-of-heart coordinate system to solve the azimuth between two points. Based on the calculation theory, the calculation model for solving the true azimuth of the baseline edge can be deduced.

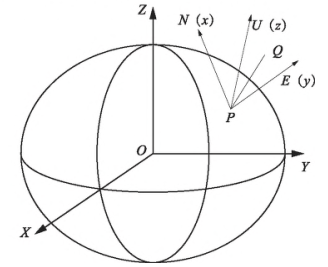
3 Calculation Examples

3. 1 Calculation based on the horizontal coordinate system of the station

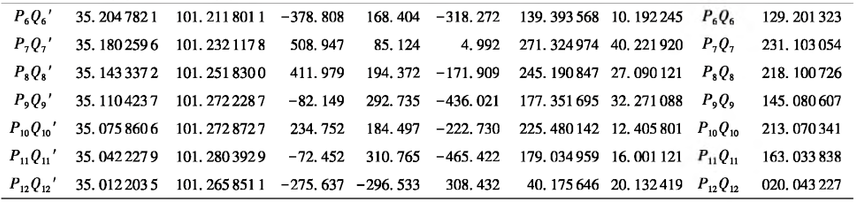
Based on the above calculation model of the station's horizontal coordinate system, with the ultra-short baseline true azimuth of an airport as the engineering background, this paper carries out field layout and observation in another measurement area, and conducts the solution test of the previous case. The base line length of the project is 50 m, and the observation accuracy is required to reach 0.005. (18 "). In this paper, the actual side length is 30-40 m, a total of 12 baselines are laid, and field GNSS observation is conducted. The results of observation and true azimuth are shown in Table 1. Firstly, GNSS observation was used to determine the geodetic coordinates (B") of the normalized points, calculate the geodetic appropriate angular coordinates of each baseline Q 'space, and obtain the values of the normalized and G 'points

The space geodetic rectangular coordinate difference (AX,Ar,AZ), the true azimuth of each long baseline Pi Q' is obtained by using the calculation model of the true azimuth of the station center horizontal coordinate system. Secondly, the TC2003 total station with nominal accuracy of 0.5 "was used to observe a (the Angle between the long baseline Q' and the ultra-short baseline E Q was observed). Finally, the true azimuth Angle of the ultra-short baseline was obtained according to the true northern position of the long baseline and a.

Table 1 True azimuth observation and solution results of the station's horizontal coordinate system

3.2 Verification based on Gaussian projection method

As for the correctness of the above solution of the true azimuth of the ultra-short base line based on the station center plane coordinate system, the traditional Gaussian projection method is used to verify it. In Gaussian projection method, the geodetic coordinates of two points on the ellipsoid are projected onto the Gaussian plane to obtain the coordinate azimuth of the baseline, and the true azimuth of the baseline can be obtained after it is transformed by the convergence Angle and direction of the meridian. In this verification example, WGS 84 ellipsoid is used, and the longitude of the central meridian is 102 when the convergence Angle of the meridian is calculated. , and the calculation results are shown in Table 2. Similarly, the true azimuth of each long baseline edge knife is calculated first, the sum of the projected coordinate azimuth and the meridian convergence Angle at the normalization point, and the direction change of the ellipsoid arc projected to the plane is the true azimuth Angle of the normalization Q/. In order to solve the complicated calculation process, this paper uses VC++6.0 platform, The solution program of the process was worked out, and the true azimuth Angle was moved to the super short PQ through the value observable connection.

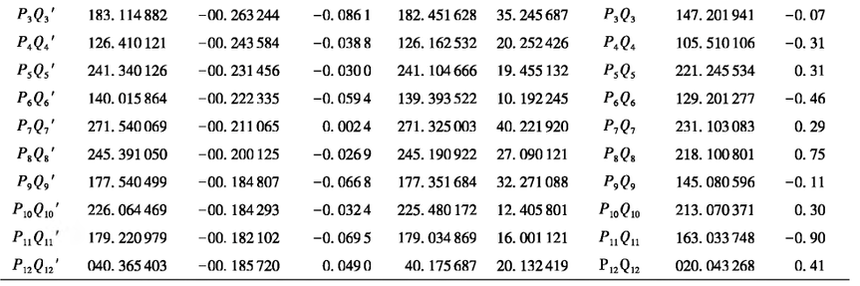
Table 2 Verification results of Gaussian projection method

4 Closing Remarks

The coordinate system is usually used for deep space geodesy, but because the origin of the coordinate system is set in the center of the station, it is helpful to derive the coordinates of the other end point of the baseline in the coordinate system of the station, so as to quickly solve the true azimuth of the baseline. From the calculation model, the most significant difference between this method and Gaussian projection method is that it avoids the tedious process of solving the convergence Angle of the meridian and changing the direction. However, although the method in this paper requires solving the spatial appropriate angular coordinates of the baseline endpoint, in practice, the GNSS static solution results already contain the baseline vector, that is, the coordinate difference of two points in the spatial appropriate angular coordinate system is obtained in Formula (1), which saves a huge amount of work for the solution of the overall true azimuth, so it is advisable to use formula (5) and the calculation formula of true azimuth. Calculate the baseline true azimuth. From the aspect of calculation, Gauss projection method is complicated and weak in practicability. The method used in this paper is simple, fast and practical. In terms of accuracy, the difference between the two methods is controlled within 1", the average difference is 0.397 ", and the results of true azimuth fully meet 0.005. (18 ") accuracy requirements. Therefore, the super short baseline true azimuth calculation method based on the station center horizontal coordinate system has obvious advantages over the traditional calculation method, and can be used in the practical production and research of similar projects.

At the same time, it should be noted that the above are all discussions on the internal solution scheme, and the accuracy of all measurement items mainly depends on the field observation. In this study, in order to ensure the observation accuracy, all observation points use forced observation pier, which not only greatly increases the measurement cost, but also makes the measurement efficiency extremely low. Therefore, in the absence of the use of forced observation pier, how to efficiently ensure the accuracy of observation, is the direction that needs attention in the future.

Reference literature

[1] SHI Yimin. Modern Geodetic control Survey [M]. Beijing: Surveying and Mapping Press,2003.

[2] Wang Jiexian, Liu Huiqin, Tang Lijun. Coordinate reduction of different stations in plane-of-heart coordinate system [J]. Engineering Survey,2005(5) : 58-60.

[3] Kong Xiangyuan, Guo Jiming, Liu Zongquan. Fundamentals of Geodesy [M]. Wuhan: Wuhan University Press,2001.

[4] Kong Xiangyuan, Mei Shiyi. Control Measurement [M]. Wuhan: Wuhan University Press,2001.

[5] Ji Kaimin, Wang Jiexian. Two methods of calculating true azimuth using geodetic coordinates [J]. Engineering Survey,2009(4) : 84-86.

[6] Li Yu, Wang Yonghong, Zhang Bo, et al. Application Analysis of Trimble GNSS Data Processing Engine (PPE) in GNSS - Short Baseline Positioning [J]. Bulletin of Surveying and Mapping,2013(2):11-14.