Research on underwater moving target location based on ultra short baseline intersection of long baseline
The location of underwater moving targets is an important parameter in oceanographic investigation, engineering detection, Marine experiments and other scientific research activities. Especially in the equipment test of Marine range, it is necessary to obtain the location information of underwater moving targets in real time and accurately. Underwater acoustic positioning technology is an effective means to obtain this information. In recent years, underwater acoustic positioning technology has been continuously developed, and the underwater acoustic positioning System has also been transformed from the traditional Long Baseline System (LBL) and Short Baseline system (Short Baseline System). SBL), Ultra-short Baseline System (USBL) to the acoustic multi-baseline combination with inertial navigation system (INS), Global PositioningSystem (GPS) and other joint positioning mode. Relevant studies show that [1-4], long baseline has the characteristics of long baseline and high positioning accuracy, but long baseline positioning is measured by accurate time delay, and the anti-range fuzzy solution ability is not strong due to the high frame rate transmission required by synchronous beacon due to the target movement. The ultra-short baseline positioning system is composed of multiple acoustic arrays and acoustic beacons. It locates by measuring distance and azimuth. Its advantages are small size and easy to use, and its azimuth parameters are not affected by distance ambiguity. Moreover, its positioning accuracy is affected by such factors as carrier installation deformation error, pose component measurement error and sound velocity error, etc., and calibration is required after each installation. The positioning accuracy of the system is not high, and it is only suitable for tracking in a wide range of operating areas [5]. In view of this, this paper proposes an ultra short baseline positioning technology based on the intersection of long baselines and buoys to achieve high precision positioning measurement of underwater low-speed moving targets.
1. System composition and key technologies
At present, the combined underwater acoustic positioning system has been widely used in China. Donghai Research Station of Institute of Acoustics, Chinese Academy of Sciences and other units [6] studied a positioning method combining long baseline and ultra-short baseline to locate underwater towed targets. However, it requires the cooperation of multiple ships in the use. The ultra-short baseline installed on the hull is susceptible to the detection of ship noise interference, especially the installation error calibration of the ultra-short baseline array and inertial components each time before the system is used. On the one hand, it is difficult to implement the measurement guarantee, on the other hand, it also brings undue measurement errors and reduces the positioning accuracy. The positioning system involved in this paper adopts the combination positioning of long baseline and ultra-short baseline, and combines the two with ocean buoy technology, which can effectively avoid the aforementioned deficiencies, especially reduce the system's noise interference from the ship, improve the azimuth detection capability of ultra-short baseline, use the long baseline to accurately distance the target from the time delay, and adopt the combination positioning based on the fusion of delay/phase difference parameters. It not only makes up for the limitation of positioning accuracy of a single positioning method, but also provides higher positioning accuracy under the circumstance that fewer positioning primitives are laid, which is conducive to the use and expansion of the system [7].
1.1 System Composition
The system is composed of buoy type underwater acoustic positioning measurement subsystem and display control subsystem, which can complete the tasks of underwater low speed target positioning measurement, test command and situation display in the sea test of the range. The sub-system is composed of long baseline underwater acoustic measuring extension, underwater acoustic measuring and processing extension, underwater acoustic synchronous beacon and underwater acoustic command machine. Buoy-type long baseline underwater acoustic measuring extension is composed of a buoy, underwater acoustic long baseline rangefinder, ultra-short baseline array, azimuth attitude inertia component, high-precision Beidou differential receiver, wireless data transmission machine, etc. The long baseline measuring array is composed of a number of buoys installed with ultra-short baseline array to locate underwater moving targets equipped with underwater acoustic synchronous beacon. The buoy measurement information is transmitted to the underwater acoustic measurement processing unit of the survey ship through the wireless link to calculate the underwater target position.
1.2 Key System Technologies
In order to meet the continuous positioning of underwater moving targets, and to overcome the shortcomings in the use of ultra-short baseline positioning on board, the system adopts the buoy, which adopts the structure design of high buoyancy and low center of gravity. After the design of impact resistance structure, it can meet the impact resistance requirements of explosion test. Synchronous beacons are installed on underwater vehicles or moving detonation sources. In order to meet the measurement needs of moving targets at different speeds, underwater acoustic synchronous beacons adopt high-gain broadband multiple access FM dual-pulse signal system with adjustable signal transmission period (0.5~5 s). The phase can obtain greater processing gain than linear FM or frequency-hopping signals in frequency bands. It can reduce the transmitting sound source level, reduce the power consumption of the system, improve the sensitivity of the system and improve the positioning accuracy. The key technologies involved in the system design are as follows.
(1) Positioning based on long baseline and ultra-short baseline data fusion
The combination of long baseline and ultra-short baseline can form a combination acoustic positioning system. The combination positioning system can usually obtain a variety of characteristic parameters of the target signal. The reasonable fusion of multi-parameter information is beneficial to improve the accuracy and reliability of the positioning system. Considering that the long baseline positioning system has a wide range of functions and high in-array positioning accuracy, and the ultra-short baseline positioning system has high integration and good short-range positioning advantages, this paper constructs the ultra-short baseline positioning system based on the intersection of long baselines, and adopts the cooperative beacon mode to conduct wide-area accurate and reliable positioning. Each node of the system is composed of a cross-type ultra-short baseline array. A time-delay/phase difference parameter fusion and baseline information fusion positioning method is proposed. The positioning optimization model based on the minimum mean square error and maximum likelihood estimation criteria is used to effectively fuse the observation information of the two parameters, so as to achieve high precision positioning of the whole measurement area.
(2) Anti-range fuzzy technology of moving target positioning at high synchronization rate
In order to obtain enough track sampling points to describe the moving process of underwater moving targets, the positioning system needs to adopt a short synchronization period. The product of sound speed and system synchronization period is called the maximum non-fuzzy distance. Taking the signal transmission period as 0.2s for example, if the sound speed is 1 500 m/s, the maximum non-fuzzy distance of the system is 300 m. When the distance between the target and the positioning array exceeds 300 m, the signal propagation delay is greater than 0.2s, while the delay value recorded by the receiving system is still within 0.2s, that is, the interval difference between the measured delay value and the real delay value is an integer multiple of the period. Correspondingly, the integer multiple of the maximum non-fuzzy distance difference between the estimated distance and the actual value is called the distance ambiguity problem. This multiple is called the fuzzy period number and solving the fuzzy period number to get the actual distance estimate is called solving the distance ambiguity. Distance ambiguity directly leads to multi-valued location results of moving targets.
Considering that the measurement of azimuth parameters is not affected by distance ambiguity, a time-delay/azimuth fusion location optimization model based on maximum likelihood criterion is adopted to transform the distance ambiguity problem into a nonlinear optimization problem under the constraint condition of azimuth parameters, and the differential evolution algorithm is used to solve the problem. Using azimuth information to limit the target area reduces the danger of the differential evolution algorithm falling into the local optimal solution. The fuzzy location of moving targets in a wide range of measurement areas can be realized without the initial target location.
(3) Accurate time delay estimation in complex shallow sea environment
It can be seen from the ultra-short baseline positioning principle that the phase measurement of underwater acoustic positioning measuring extension is mainly completed by measuring the phase difference between sound base interval elements. Its essence is the measurement of time delay difference. The prerequisite for accurate measurement of time delay difference is to accurately measure the time delay of each element. Generally speaking, energy detection is used to estimate the time delay of single frequency signals. The frequency modulation signal mostly adopts copy-coherent mode to detect the signal front. The acoustic channel in shallow sea is a more complex multi-path coherent channel. The signal arriving at the receiving end after multipath transmission is significantly different from the transmitted waveform, and the direct sound and reflected sound constantly change with the change of relative distance. Signal reverse stacking results in a very small signal amplitude in the stacking part, so the signal at the front end of the receiver presents a "edge" phenomenon. In this way, the direct sound is easy to miss the alarm, which makes the detection delay value of the system jump significantly. For acoustic array, if the effective pulse delay value of each array jumps randomly, the positioning accuracy of the system will be seriously affected. The system uses the means of initial measurement and precision measurement to adopt secondary time delay estimation for the received signals, so that the accuracy of time delay measurement between each channel is guaranteed within 1 second, which can well solve the accurate time delay estimation in the complex shallow sea environment.
(4) Reduction and elimination of ultra-short baseline array error in buoy mode
The ultra-short baseline array is located by the phase difference. The design and calibration of acoustic array directly affect the phase difference between signals. The initial phase and installation position deviation between sound base bursts are the key factors that directly affect the positioning accuracy. The initial phase between the sound base interval elements will directly bring phase measurement error, which belongs to the systematic error. It needs to be calibrated in the anechoic pool or open water before leaving the factory, and then corrected to the phase difference measured by the array, so as to reduce the impact on the positioning accuracy of the whole system. The rotation Angle error between acoustic array coordinates and geodetic coordinates is difficult to be directly measured, which is mainly caused by installation error, and can be calibrated by the method described in reference [8]. Buoy is adopted in the system, and the ultra-short baseline array is fixed under the buoy, which can only be calibrated once, to avoid the disadvantages of adaptability calibration after each installation of shipborne array and low test efficiency.
2. Research on system information fusion localization algorithmLong baseline and ultra short baseline work independently of each other, and the measurement information is obtained according to the following criteria according to the above model.
(1) When the number of effective buoys (long baseline primitives) is large enough (no less than 3), the positioning model is dominated by long baselines, and the ultra-short baselines provide phase difference parameter information, which is mainly used for range ambiguity resistance and fusion weighting processing of the redundant array ranging information.
(2) When two buoys are used, the method of long baseline is used to solve the problem, and the information of phase difference parameter is used to judge the double solution of the ultra-short baseline.
(3) When the single buoy receives the target signal, the ultra-short baseline is directly used to solve the problem, and the true solution is identified according to the measured historical position information, and the fuzzy solution is proposed;
(4) For the phase ambiguity problem of the ultra-short baseline, it is solved through optimization design in the array design. Phase deconvolution is realized by using the phase information of two array elements with less than half wavelength to eliminate the phase fuzzy solution.
In this paper, it is assumed that the two systems work at the same time, and a total of 5 groups of positioning results can be obtained, including 1 group of long baseline results and 4 groups of ultra-short baseline results. The key of location result fusion is how to combine 5 groups of information effectively so that the location result of fusion is better than that of a single system.
2.1 Minimum mean square error estimation and maximum likelihood estimation
In mathematical statistics, mean square error refers to the expected value of the square difference between the estimated value and the true value of the parameter, which is denoted as MSE. It is a convenient method to measure the "mean error" and can evaluate the degree of change of the data. The smaller the mean square error value, the higher the accuracy of the results described by the prediction model.
Under the condition that X and Z are known to be two random vectors, and there is a joint probability density function between them, the estimation that minimizes the sum of the mean square error of each estimation component is called the minimum mean square error estimation X plus V. The sum of the mean square errors of the estimated components can be expressed as follows.
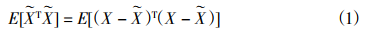
Maximum likelihood estimation is a statistical method based on maximum likelihood principle and an application of probability theory in mathematical statistics. Maximum likelihood estimation provides a method of "the model is established, the parameters are unknown". By observing the results of several tests, a certain parameter value can be obtained by using the test results to maximize the probability of sample occurrence.
2.2 Time-delay/phase difference parameter fusion positioning optimization model based on the least mean square error criterion
It can be seen that the positioning accuracy of fusion results is no less than the positioning accuracy of each system, and the fusion method based on the minimum mean square error criterion is feasible.
2.3 Time delay/phase difference parameter fusion localization optimization model under maximum likelihood criterion
The time delay/phase difference parameter fusion combined baseline positioning method is to effectively fuse the observation information of the two parameters by constructing the optimal positioning model under the maximum likelihood criterion, so as to realize the high-precision positioning of the whole measurement area.
3 Analysis of system positioning accuracy
In order to verify the positioning accuracy of the combined positioning measurement, this paper simulated the positioning accuracy of the long baseline, ultra-short baseline and long baseline/ultra-short baseline combination positioning respectively, and simulated two time-delay/phase difference parameter fusion algorithms based on the minimum mean square error criterion and maximum likelihood criterion respectively in the combined positioning mode. Specific simulation conditions are as follows.
(1) Position accuracy of buoy (array element) (Beidou /GPS positioning accuracy: 3m);
(2) The error of sound velocity measurement is 2.
(3) The delay measurement error is 200 seconds;
(4) The phase difference measurement error is 2.2 Yi;
(5) The ultra-short base interval is 0.25m, and the array installation error is 0.6mm;
(6) The number of Monte Carlo statistics is 2000.
Figure 3 to Figure 6 respectively show the positioning accuracy of the two fusion algorithms under long baseline, ultra-short baseline and combined positioning.
It can be seen from the simulation results that the positioning accuracy of the long baseline is higher for the positioning accuracy of the center of the array because it can obtain accurate time delay estimation. The remote positioning accuracy of the ultra-short baseline is lower, but the local positioning accuracy is higher. The positioning accuracy of the combination positioning of the long baseline/ultra-short baseline is higher than that of the long baseline in the position near the array element, and the positioning accuracy of the distant position is higher than that of the ultra-short baseline. The positioning accuracy after data fusion processing using the two criteria is almost the same in the center of the array. The precision of the combination positioning based on the minimum mean error criterion is higher than that of the maximum likelihood estimation criterion in the near position of the array element. On the whole, the combination positioning method can fully combine the advantages of long baseline action distance and ultra-short baseline high local accuracy. The positioning accuracy of this method is higher than that of a single method on the whole.
The underwater moving target is a dynamic target with a certain speed, and its influence on signal detection is reflected in the Doppler effect of the signal received at the receiving end, and the frequency will be offset to a certain extent, resulting in the delay detection deviation. The simulation calculation and analysis show that for the underwater acoustic signal with a signal frequency band of 20~30 kHz and a pulse width of 10 ms, the target speed is
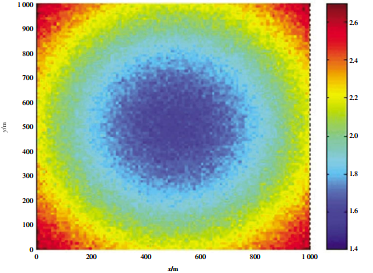
FIG. 3 Positioning accuracy of long baseline
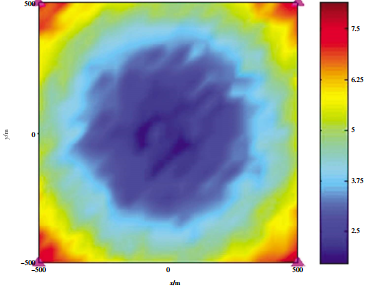
FIG. 4 Positioning accuracy of ultra-short baseline
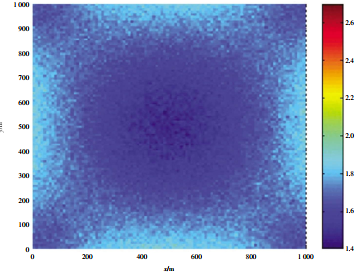
Figure 5 Combined positioning accuracy based on the minimum mean square error criterion
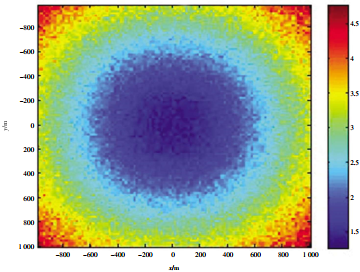
Figure 6 Combined positioning accuracy based on maximum likelihood estimation criteria
At 2 kn, the delay measurement error is about 200 seconds. When the target velocity is 4 kn, the delay measurement error is about 400 seconds. When the target velocity is 6 kn, the delay measurement error is about 600 seconds. When the target velocity is 8 kn, the delay measurement error is about 800 seconds. Accordingly, this paper further simulated and verified the positioning accuracy of stationary target with a speed of 0 kn (FIG. 7) and moving target with a speed of 8 kn (FIG. 8) under the combined positioning mode. The specific simulation conditions are as follows: Except that the delay measurement error of moving target with a speed of 8 kn is 800 seconds, other simulation conditions remain unchanged.
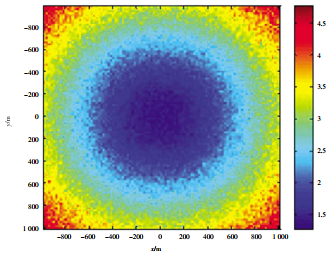
Figure 7 Positioning accuracy of underwater stationary target (speed 0 kn)
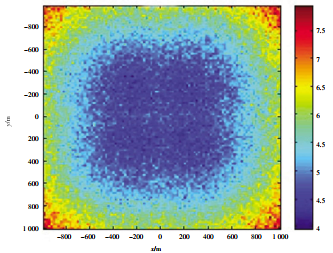
Figure 8 Positioning accuracy of underwater low-speed moving target (speed 8 kn)
The simulation results show that within the range of 2km, the horizontal positioning accuracy of the static target is no more than 2 R (R is the measurement slant distance), and the horizontal positioning accuracy of the dynamic target is no more than 4 R considering the Doppler migration and timely delay measurement error of the dynamic target, which can meet the measurement requirements of the system.
4 Conclusion
In this paper, a long baseline/ultra short baseline combination positioning system based on buoys is proposed to locate underwater moving targets. The adoption of buoys overcomes the disadvantages of large installation errors in the combination of ultra short baselines on ships, avoids the need for attitude adaptive calibration every time after installation, and improves the measurement accuracy. At the same time, the combination positioning method can effectively reduce the number of long baseline elements and improve the test efficiency. The time delay/phase difference parameter information is used to solve the problem of distance ambiguity caused by high frame rate and cross-period synchronization beacon by the fusion method based on the minimum mean square error criterion and the maximum likelihood estimation criterion, which improves the positioning accuracy of moving target. Finally, the spatial distribution of positioning accuracy of each method is simulated and analyzed, and the positioning accuracy of this method is better than that of a single system. This method does not need to calibrate the matrix before each test, and has the advantages of high efficiency, simple test preparation and high quality and efficiency measurement. At present, the system has been successfully applied in the shooting range.



