Research on fuzzy algorithm of phase difference solution for ultra short baseline underwater acoustic positioning system
Signal Direction of A rriv v l (D O A) estimation has important application value in radar, sonar, communication and other military and civilian fields. The ultra-short baseline underwater acoustic positioning system estimates the direction of signal wave by measuring the phase difference between the receiving elements, thus realizing the positioning of underwater targets [4]. When the interval between the elements is larger than half wavelength of the signal, the measured phase difference may be an integer multiple of 2n from the real phase difference, which is called phase difference ambiguity. The multiple is called fuzzy number, and the process of solving fuzzy number is called unambiguity. Phase difference unambiguities are the key problem to realize accurate positioning of ultra short baseline system.
In engineering applications, the combination of shorter baseline and longer baseline with less than half wavelength is usually used to eliminate phase difference ambiguity. When the measurement error is constant, its performance decreases with the increase of the ratio of longer baseline to shorter baseline length. In addition, when the signal frequency is high, considering the problems of occlusion and coupling, it may be difficult to realize the array configuration of half wavelength spacing. By constructing multivariate non-uniform array, the phase difference resolution can be realized by using the length relationship of multiple baselines [5~7], and the minimum array spacing can exceed half wavelength. Based on the remainder theorem method [8], the fuzzy number of the longest baseline can be obtained directly in theory, but the length of the baseline is required to be pair-to-pair prime and sensitive to noise. By constructing virtual baselines with less than half wavelength, the fuzzy number of other baselines can be solved step by step. This method is usually only applicable to specific formations, and the fuzzy solving performance is greatly affected by the phase difference error and the ratio of the length of each baseline. The multigroup ratio method [1] firstly uses the length ratio of adjacent baselines to solve possible combinations of fuzzy numbers, and then obtains a set of common fuzzy numbers, whose performance is affected by the maximum common factor of the length of adjacent baselines. The correlation search method [1213] establishes the similarity cost function between the theoretical reference data and the measured phase difference, and selects the Angle that minimizes the cost function as the signal direction through the grid search method. When the grid division is large, it is easy to produce the mismatch between the theoretical data and the actual phase difference, which leads to the failure of unambiguation. However, when the grid division is small, the storage space and computation amount are increased, and the efficiency of the algorithm is reduced.
In addition, the existing multi-baseline deblurring methods usually regard the measurement error of phase difference between baselines as statistically independent, and the direction finding results are usually obtained by using the longest baseline or a part of the baseline estimation, and the estimation accuracy is local limiting. In literature [14], the correlation between phase difference measurement errors was considered and the least square method was used to estimate the Angle of reach, but the fuzzy phase difference was not considered. In this paper, the phase difference fuzzy problem is transformed into multiple compound hypothesis testing problem by using the statistical characteristics of the phase difference measurement error, and a fuzzy solution method based on the generalized maximum likelihood criterion is proposed. Based on the longest baseline measurement phase difference, the fuzzy number vector initialization method reduces the number of multi-dimensional integer search. In this paper, the observable condition of the Angle of reach is deduced and its estimation accuracy is analyzed theoretically. The algorithm effectively increases the aperture of the unfuzzy array, and has low requirements on the formation. It makes full use of the observation data of phase difference, and can realize the high precision estimation of signal direction.
2. Phase difference fuzzy problem description
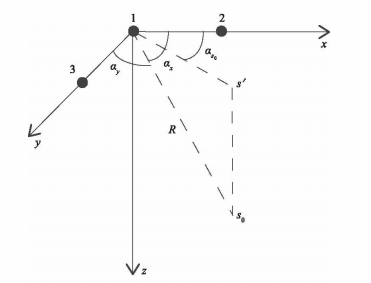
As shown in Figure 1, the positioning principle of the ultra-short baseline system [15], three elements are located on two mutually perpendicular baselines, and the length of the baselines is that element 1 is located at the origin of coordinates. Suppose the target is located at S ○, its horizontal position coordinate is [X, Y] T, and the measured oblique distance between the target and element 1 is the center

Where, ax and ay are the included Angle between the target position vector and the X-axis and the Y-axis respectively, y is the projection of S on the x-y plane, and the included Angle between the position vector and the X-axis aS ○ is the horizontal azimuth Angle of the target, and
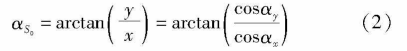
ax and ay can be obtained by measuring the phase difference between array 1 and array 2 and the phase difference between array 1 and ψ3 respectively, i.e
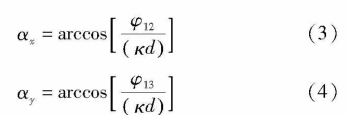
Among them
png indicates the signal wave number and image.png indicates the signal wavelength
f0 is the signal frequency, which is visible for the speed of sound in water. Accurate measurement of signal reach Angle a x and ay is of great significance for improving the positioning accuracy of the ultra-short baseline system. Increasing array spacing is usually conducive to improving the estimation accuracy of reach Angle, but when d> λ/2, 2n ambiguity may occur in the measurement phase difference, that is, phase difference ambiguity. Fuzzy phase difference will further lead to fuzzy positioning. Therefore, fuzzy direction finding is the key problem to realize accurate positioning of ultra-short baseline system. This paper focuses on this problem. Considering that the estimation process of the Angle of reach of the two arrays is relatively independent, in order to facilitate the analysis, a set of arrays is used as the model to describe the phase difference fuzzy problem and to study the fuzzy solution algorithm. Without loss of generality, the binary array composed of element 1 and element 2 is considered, and the phase difference between the two elements is.

Where, a e [0, n] is the Angle between the signal signal direction and the positive direction of x axis. Suppose the measurement phase difference is less e (-n, n), then
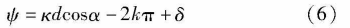
Where, is the phase difference measurement error, and the integer is the fuzzy number
As can be seen from equation (6), when d > λ/2, the phase difference ambiguity problem leads to the measurement phase difference corresponding to multiple possible signal direction, but only the Angle corresponding to the true fuzzy number is the estimated value of the Angle of reach a. The purpose of unambiguation is to compensate the measured phase difference by obtaining the real fuzzy number, and then to estimate the human Angle of the signal.
3. Estimation algorithm of unfuzzy-solving Angle of reach based on generalized maximum likelihood criterion
3. 1 Theoretical model
(M-2) auxiliary elements are added between the two arrays whose spacing is more than half wavelength to form the M-element non-uniform linear array, and the minimum spacing is more than half wavelength. Take the MTH element as the reference to form the baseline, as shown in Figure 2
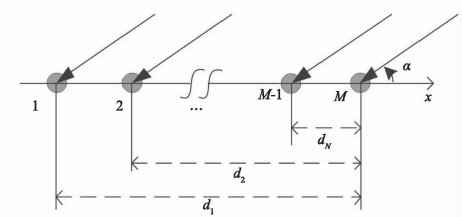
For the NTH baseline, there is
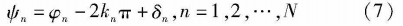
Then the observed data can be written as follows:
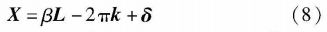
As can be seen from Equation (8), a group of phase difference observations of the array correspond to a variety of possible fuzzy number vectors, but only the Angle corresponding to a true fuzzy number vector is the estimated value of the true direction of the signal. Therefore, the key of the problem is how to distinguish the real fuzzy number vector from many possible fuzzy number vectors. In this paper, the fuzzy solving problem is transformed into multiple compound hypothesis testing problem, and each possible fuzzy number vector is matched with different hypothesis conditions, then the correct fuzzy solving is realized by judging the corresponding hypothesis of the real fuzzy number vector to be true.
3. 2 Fuzzy number vector initialization
Theoretically, all fuzzy number vectors can be obtained through multidimensional integer search, but the fuzzy number vectors obtained in this way have a lot of redundancy, which greatly increases the complexity of solving the subsequent hypothesis testing problem. In the following, on the basis of fully mining the Angle information of signal in the phase difference observation data, the initialization method of fuzzy number vector in this paper is given.
According to Equation (7), the expression of the fuzzy number of the longest baseline of the array in Figure 2 is

Let the set of supplementary phase differences be
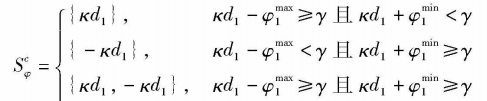
The fuzzy number of each baseline is estimated
The image.png expression can be substituted into Equation (11) and combined with equation (7)
The following is the construction of multiple compound hypothesis testing model to distinguish the real fuzzy number vector in this group of vectors, so as to achieve the fuzzy solution.
3. Construction of multivariate composite hypothesis testing model and algorithm implementation
The probability density function of Hq is
To sum up, the specific implementation steps of phase difference degumming algorithm based on generalized maximum likelihood criterion are summarized as follows:
(1) The set Sψ is obtained by the operator f, and the set is obtained by equation (10)
(2) According to Formula (11), the fuzzy number of each baseline is estimated by the elements in the set, so as to initialize the fuzzy number vector.
(3) Construct a multivariate composite hypothesis testing model by using the fuzzy number vector obtained in step (2), calculate the test statistics under each hypothesis, as shown in Equation (9), and determine that the minimum hypothesis is true. Finally, the Angle estimate is obtained by modifying the formula (22).
4 Algorithm performance analysis
4. 1 Analysis of the observability of the Angle of reach
Firstly, the condition of Angle estimation without mode paste in the range [0, n], that is, the observable Angle of reach, is given. Suppose the length of N baselines in FIG. 2 is d "= doPn, d1 > d2 >... > dn, where d is a positive rational number, and is a positive integer, then the following conditions must be met when the Angle of reach can be observed:
(1) P1, P2... PN is a decreasing positive integer with the greatest common factor of 1.
(2) do < λ/2
The proof is as follows: without considering the interference of noise, it can be obtained respectively under the hypothetical condition Hq and Ht
The algorithm only works for certain formations. Compared with the two, the algorithm in this paper has more relaxed requirements for the meta distribution, which is easier to achieve in practical applications, and the algorithm has strong universality.
4. 2 Accuracy analysis of radar Angle estimation
Let there be no fuzzy phase difference vector
And the joint probability density function of X prime is
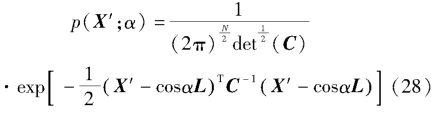
Then F is h e r of X 'is
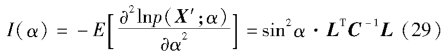
The Cramer-Rao Bound (CRB) is estimated to be
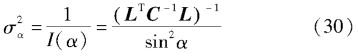
Under the condition of a certain phase difference measurement error, the mean square error of Angle estimation of the proposed algorithm is approximately CRB. Therefore, compared with the traditional fuzzy-solving direction finding method which constructs the interval of array elements smaller than half wavelength, the proposed algorithm effectively increases the aperture of the fuzzy-free array, takes into account the correlation between the phase difference measurement errors, makes full use of all baseline observation data, and has a higher accuracy in estimating the Angle of reach
5 Simulation Analysis
In order to verify the performance of the proposed algorithm, M o te C a rlo repeated tests were used to calculate the probability of correct fuzzy resolution and direction finding errors. Monte C a rlo test number was set as Jin muscle, and iVMC = 1 0 0 0 in simulation. If each baseline fuzzy number is equal to the corresponding real fuzzy number, it is called correct fuzzy solution, then the probability of correct fuzzy solution refers to the ratio between the number of correct fuzzy solution and Wmc. The Root Mean Square E rro r (RM SE) error of Angle estimation is
The conditions are as follows: The signal is a C W pulse, frequency f0= 75k H z, underwater sound velocity c = 1500m/s, and signal wavelength λ =0.02m. The five-element linear array is designed by referring to the requirements of the stepwise method in reference [9]. The right-most array is taken as a reference, and the baseline length vector d= [45do, 33do, 18 do] T. It is easy to verify that the array arrangement satisfies the observability condition of the proposed algorithm for reaching Angle, and the array spacing exceeds half wavelength
6 Conclusion
Aiming at the fuzzy problem of phase difference faced by ultra-short baseline underwater acoustic positioning system, a multi-compound hypothesis testing model is constructed in this paper, and a phase difference solving fuzzy algorithm based on generalized maximum likelihood criterion is proposed. The observability and estimation accuracy of the Angle of reach are analyzed theoretically and verified by simulation. The results show that the proposed algorithm does not need to construct the array with less than half wavelength spacing required by the traditional algorithm, effectively enlarges the aperture of the fuzzy-free array, has lower requirements on the collocation of elements, has higher universality, and can effectively eliminate the phase difference ambiguity. The algorithm uses the phase difference observation data to initialize the modulus number vector, reduces the number of multidimensional integer search, and makes full use of the statistical characteristics of the phase difference observation data, and the direction finding accuracy can be close to CR B. Compared with the previous methods, the fuzzy solving performance and direction measurement accuracy are higher under the same conditions, and no grid search is required. In addition, although this algorithm is proposed to solve the phase difference mode paste problem in ultra-short baseline positioning based on narrowband signal, its basic idea can also be extended to solve the phase difference fuzzy problem in broadband ultra-short baseline positioning, but the specific processing process needs to be adjusted according to the actual application conditions. Limited by space, this paper will not be narrated, and relevant issues will be studied in the follow-up work.



