High precision error compensation algorithm for diffused silicon pressure sensor

The transmission characteristics of the diffused silicon pressure sensor are greatly affected by temperature, so the input pressure and temperature of the sensor must be decoupled by some means, so as to achieve effective compensation for the output of the pressure sensor and obtain accurate and reliable pressure measurement value. In this paper, the error composition of a general diffused silicon pressure sensor is analyzed, and a simple and high-precision compensation model for the error is proposed, and an effective formula is established. Finally, the correctness of the algorithm is verified by an example, and its accuracy can reach less than 0.1% FS.

A sensor is a device or device used for physical measurement and is widely used in real life and various production fields, including automatic control systems for industrial processes. Pressure is one of the most common physical quantities, and its measurement is one of the most important links in the industrial process control system. Therefore, the research of improving the performance of pressure sensors has been highly valued at home and abroad. At present, the commonly used pressure sensors mainly include strain pressure sensor, piezoresistive pressure sensor, capacitive pressure sensor, piezoelectric pressure sensor and harmonic vibration type pressure sensor. Piezoresistive sensors are made using the piezoresistive effect of semiconductor materials. It has the characteristics of high resolution, good dynamic response, easy to develop in the direction of intelligent and energy-saving integration. With the continuous progress of silicon microcomputer processing technology, piezoresistive pressure sensors have been rapidly developed and become the most widely used pressure sensors at present. They are also widely used in industrial process control systems. Pressure transmitters from companies such as ABB and Foxboro all use diffused silicon pressure sensors. However, due to the temperature sensitivity of the manufacturing process and the diffused silicon itself, the diffused silicon pressure sensor has a large error. With the growing popularity of intelligent instruments, software compensation, which is superior to hardware compensation, has been widely accepted. Commonly used software compensation methods include lookup table method, interpolation method, test general formula and so on. Compensation based on multinomial formula fitting is also a very common method. However, the general method has a great limitation, this paper is aimed at this problem put forward a better solution.

1. Computational analysis

1.1 Error difference analysis

Diffused silicon pressure sensor has a large temperature shadow, so it is necessary to use some means to decoupled the input pressure and temperature of the sensor, so as to achieve effective compensation for the output of the pressure sensor. Get accurate and reliable pressure measurements. By conducting input/output (P-U) experiments on a large number of diffused silicon pressure sensors at different temperatures, a series of input/output curves can be obtained, as shown in Figure 1.

Figure 1 Input and output diagram of diffused silicon pressure sensor

As can be seen from Figure 1, there are three main errors: zero error, nonlinear error and temperature drift error. The first zero error is mainly caused by the fact that the resistance values of the four resistors of the differential bridge are not exactly equal. With the continuous development of industrial technology, this error is getting smaller and smaller, but it is still in a degree that cannot be ignored. The second nonlinear error is mainly caused by the difference in the mental sensitivity of the pressure of the four resistors of the differential bridge, which is also inevitable in the process technology, because the diffusion concentration of the diffused silicon can not be 100 percent accurate. So there's no way to eliminate this error. The third kind of temperature drift error can be divided into two parts: one is the zero point temperature drift error. It is caused by the different sensitivity of the four resistors of the bridge to temperature. In the absence of pressure input, the difference in the resistance change of each bridge caused by the same temperature leads to the output of the sensor: the second is the mental sensitivity temperature drift error, which is produced as a result of the use of pressure and temperature together, and a certain pressure becomes the next. The difference in the influence of different temperatures on the sensitivity of the bridge resistance results in a large output deviation of the sensor [2-5]. The compensation calculation method must compensate these partial error difference effectively.

1.2 Mathematical model and formula of error compensation

Starting from the three main errors of pressure sensor, the mathematical model of error compensation is proposed in reference 21

The specific formula is:

From the analysis of its progress, it can be seen that U (P, t) in equation (1) is the output of the sensor, R (f) is the zero drift and zero temperature drift table, and n is in equation. That is, the zero drift error, n + van t is the zero temperature drift error; (P) is a nonlinear error table expression; F2(f) is a temperature-sensitive drift meter. Although the model contains all the major errors that need to be compensated, it can be seen from the systematic calculation method presented in this paper that the model compensates for zero and full scale errors. The error difference compensation of the middle range is rough, so the compensation effect may not be very reasonable. In view of this situation, this paper proposes a new mathematical model:

Usually in practical applications, the temperature is expressed by relative temperature, then equation (3) becomes equation

Where, A t=t - to(fo is room temperature).

To approximate the objective function by polynomial, usually one approximation is far from enough, so quadratic approximation is used. The specific formula is established as follows:

Compared with the model in literature [2], this model adds the description of the intermediate range, which makes the error compensation more accurate. In order to facilitate the conversion of the formula, the formula (5) can be rewritten into the formula (6) :

According to the method discussed in literature [2], formula (6) is transformed into a function of input P as output / 2, and thus:

The method of determining the coefficient of the formula is as follows:

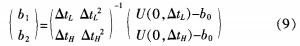
If the sensor with a relatively large error is encountered, in order to achieve the required accuracy, the algorithm can be easily extended, for example, to add a correction point p= 0.4 when the temperature is equal, only the following adjustments are required for equation (6) :

That is, a small term is added to the second term of the formula, and the appearance of the new coefficient A will not have any effect on the original coefficient. If you want to add another temperature point equal at p= 0.6, you only need to make the following adjustments to equation (17) :

2 Example application analysis

First, the pressure of a typical diffused silicon pressure sensor with a full scale of 600kPa was measured at three different temperatures. At A certain temperature, there is a measuring point every 50 kp-a, and the corresponding output pressure is measured at each measuring point. Table 1 is obtained after data normalization.

The original error analysis was calculated using the general formula (19), and the error results in Table 2 were obtained

According to the error analysis, the zero drift error, zero temperature drift error, mental sensitivity drift error and nonlinear error of the sensor are serious, and the overall error error can reach 5% FS water level. This is not acceptable in practical application. First, the original measurement data is normalized. The measurement errors of zero and full scale points at the reference temperature can be directly eliminated, and then the error compensation of the remaining measurement points can be carried out according to equation (16). The coefficients calculated from the above equation are as follows:

The final results are shown in Table 3.

Table 3 Sensor input and output data after compensation

In equation (19), U (P, A t) is replaced by P (X, A t), error analysis is carried out, and the percentage error error of sensor output after compensation is obtained, as shown in Table 4. It can be seen that the error of each item has been greatly improved after compensation by this algorithm. The overall error reaches the water level below 0.1% FS.

The error compensation algorithm of diffused silicon pressure sensor proposed in this paper has many obvious advantages. First of all, the form of the algorithm is irregular and simple, the system calculation is irregular, and it does not need to calculate the torque matrix with huge workload. Its second point is very suitable for MCU implementation, it does not need a lot of space to store lookup table data, there is no complex calculation of common formulas, only a few simple parameters and a simple equation, and the compensation effect is very good after detection. Generally, it can reach less than 0.1% FS, which has certain practical value.

References:

[1] LI Guoyu, Sun Yicai, Dai Zhenqing. Intelligent pressure sensor with output signal based on normalized polynomial fitting fJ]. Automation Instrument, 2005, 26 (1) : 29-33.

[2] Ark Kay, M ikhail Ivanov, V iola S ehaf er. A practical technique fo r m inim izin g th e n u m b er o f m e asu rem e n ts in se n sor sign a l cond itioning  calibration [J]. T exas In strum ents Int A p plication R e p ort S B O A 1 1 1, 2 00 5, 6:1-8.

[3] MAX IM Inc. A pproaches f or com p ensating span and offset in pressure sensors[J]. S en sor Signal C on ditioners A pplication, 2 00 1. 7 4 3:2-5.

[4] MAX IM Inc. Sensor tem perature com p ensa tion using the four D A C signal conditioning arch itecture. [J]. Sensor Signal C ondition ers A p p lic a tion N ote 18 3 9, 2 0 0 2:2-8.

[5] Eric Perraud. T heoretical m odel of per f orm ance of a silicon piezoresistive pressure sensor III. Sensors and A ctuatom, 1996, 57 (3) : 245-252.