Research on temperature compensation technology in high precision pressure sensor
0 Introduction
Piezoresistive pressure sensor is a kind of pressure sensor made of semiconductor piezoresistive effect, which has the characteristics of small size, high precision and good stability, and is widely used in electric power, petrochemical, automotive electronics and other fields. However, the silicon piezoresistive film, as its core, is sensitive to temperature changes, resulting in zero point temperature drift, affecting the sensitivity of the sensor. There are two common temperature compensation methods: hardware compensation method and software compensation method. However, the traditional compensation method based on the hardware characteristics of the sensor has some shortcomings such as difficult debugging, low precision and poor versatility, so it has no practical application in engineering. Software compensation technology can solve these problems well, so people pay more and more attention to it.
1 High precision pressure detection system based on software compensation
Software compensation is the combination of microprocessor and pressure sensor, make full use of the rich software functions of microprocessor, and correct the error caused by the temperature of pressure sensor through a certain compensation algorithm. Regardless of which software compensation method is used, the architecture of the hardware system is similar, the difference is in the algorithm. We designed a high precision pressure detection system using LPC2478 as the central processor. The main frequency is up to 72Mz, the on-chip flash program memory is up to 52k, and serial ports are abundant. At the same time, the system uses ultra-high sampling accuracy A-D, and is configured with A SDRAM.
2 Algorithm analysis and implementation
At present, software compensation methods mainly include interpolation method, curve and surface fitting method, table lookup method and BP neural network method. In the interpolation method _3, the data is assumed to be correct and some method is needed to describe what happens between the data. Curve fitting methods try to find a smooth curve that is the best fit to the data, but does not need to go through any data points. The table lookup method is to preload a series of parameters into the parameter table,
After the measurement data is obtained, it is processed according to the corresponding parameters. Table lookups take up a lot of storage and are not suitable for microprocessors. Artificial neural network model is established and network parameters are determined by sample training. The biggest disadvantage is that the network is unstable and the training time is long. In this paper, a compensation algorithm combining curve fitting and three-spline interpolation is proposed, which can significantly improve the compensation performance.
2.1 Polynomial fitting
Among the curve fitting methods, polynomial fitting is the most suitable fitting method, because polynomial fitting has the advantages of easy calculation and good fitting effect. n, make an m polynomial (m "n")

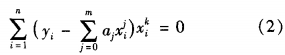
Equation (2) can be expanded to a linear system of coefficients, which has a unique solution, that is, the coefficients of the polynomial to be fitted.
2. 2 Cubic spline interpolation
Spline interpolation is an improved piecewise interpolation, which constructs a spline function between the cells of each adjacent node. At the same time, in order to ensure the continuity at the node, there is a second order smoothness at the node, that is, a continuous second order derivative. The cubic spline interpolation function is defined as follows:

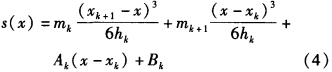
The expressions for Ak and Bk are obtained by substituting the two node values of Xk and Xk+1:
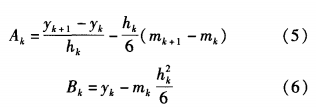
As can be seen from equation (4) and (6), only m (k = 0, 1,... n), then we get s(x).
2.3 Temperature compensation model
The pressure sensor is generally at n standard temperature t, m standard pressure Pj(j = 1, 2,... , m), and obtained the n ×m group standard points. Based on the measured data pairs (ti, pj, uij) of the pressure sensor obtained in the calibration process, the functional relationships of the three are obtained through appropriate algorithms as follows, where the output voltage of the pressure sensor is referred to.

For this temperature compensation model, the temperature compensation algorithm steps combining curve fitting and cubic spline interpolation are given:
1) With constant temperature t1, pressure P and voltage M are fitted by a quadratic curve, and the relationship curve between the two is obtained: P = f(u); With constant temperature t2, pressure P and voltage u were fitted by a quadratic curve, and the relationship curve between the two was obtained: p =f (u); And so on, until the fixed temperature t is constant, the quadratic curve of pressure P and voltage is obtained: p =fn (u). The fitting of conics can be realized by programming in ATLAB.
2) In the actual measurement process, the measured voltage is substituted by P = f1(u), P =f2 (u),... Where, P = fn(u), the pressure value at n standard temperatures is obtained;
3) The above pressure value and standard temperature are interpolated by cubic spline, and the correlation curve of pressure P and temperature t is obtained. The cubic spline interpolation is implemented in RM through C programming language;
4) Substitute the real-time temperature value measured by the temperature sensor into the above curve to obtain the temperature compensated pressure value.
2.4 Analysis of experimental process and results
Table 1 shows the output voltage value of the sensor at the pressure and temperature standard points.
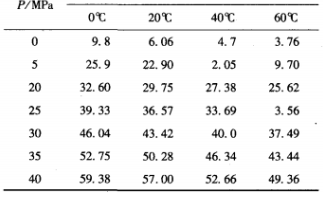
Table 1 Experimental calibration data
According to the above algorithm steps, the experimental data are processed. First of all, the fixed temperature is unchanged, and the quadratic fitting of P and u is obtained:

It can be seen from the fitting results that the sensor used in the experiment has good linear characteristics under the condition of fixed temperature. The test was carried out at four temperature points respectively, 8.2 ℃, 4.6℃, 22.3 ℃ and 36.5 ℃, and the results after temperature compensation were shown in Table 2.
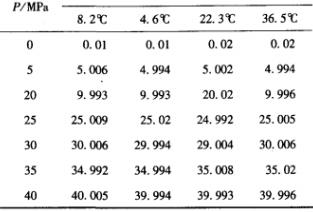
Table 2 Pressure value after warming
The results show that the performance of the system can be improved significantly by using the compensation method of curve fitting and cubic spline interpolation. Meanwhile, the temperature compensation performance can be further improved by increasing the pressure and temperature standard points.
3 knots
The temperature compensation method proposed in this paper, which combines quadratic curve fitting and cubic spline curve interpolation, can achieve high precision temperature compensation under the condition of fewer calibration points, thus effectively reducing the sensor calibration time and workload. If the accuracy of pressure sensor is put forward higher requirements, under the premise of fully considering the cost, hardware computing power and running speed, the system performance can be improved by increasing the standard point method, which has certain theoretical significance and engineering application value for solving the temperature compensation problem of high-precision pressure sensor.
References:
[1] LI Qiang, Liang Li, Liu Zhen et al. Intelligent Pressure Sensor System with temperature compensation work [J]. Chinese Journal of Scientific Instrument, 2008 (29) : 1934-1938.
[2] Liu Song. Research and Design of Intelligent Pressure Detection System [D]. Tianjin: Tianjin University: School of Electronic Information Engineering, Master's thesis, 2006:35-46.
[3] Wang Pitao, Zhai Diantang, Cheng Xiefeng. Temperature compensation of pressure sensor based on cubic B-spline interpolation [J]. Information Technology and Informatization, 2007 (3) : 112-LL5.
[4] Sun Zhizhong, Yuan Weiping, Wen Zhenchu. Numerical analysis [M]. Nanjing: Southeast University Press 2003:16-21.
[5] JA SO N Palmer. P recise Pressure Sensor Temperature Compensation A lgorithms[D] : M aster T hesis. New Y ork: State U niversity of New Y ork, 20 06:67-75.
[6] Zhang Yanfeng, Yan Jiaming. Temperature compensation algorithm of pressure sensor based on least square method [J]. Computer Measurement and Control, 2007, 5 (2) : 1870-1874.



