Design and analysis of MEMS pressure sensor based on signal-to-noise ratio
0 Introduction
MEMS piezoresistive pressure sensors with their advantages of small size, low cost and high performance are widely used in electrical appliance manufacturing, automobile industry, biomedical, meteorological observation and aerospace and other fields. The research of MEMS piezoresistive pressure sensor mainly focuses on sensor sensitivity, linearity and range. With the improvement of measurement requirements, higher requirements are put forward for sensor resolution. Noise determines the minimum detectable signal of the sensor, which is one of the important factors affecting the performance of the pressure sensor.
In order to explore the influence of the structure of MEMS pressure sensor varistor on the signal-to-noise ratio, the structure of MEMS silicon piezoresistive pressure sensor is designed and analyzed. Firstly, ANSYS simulation was used to explore the stress distribution of each structure sensor under pressure, and the sensor noise and signal-to-noise ratio of each structure was calculated through the simulation data. Then, SOI (silicon on insulator) is used to make part of the sensor chip, and the raised varistor is introduced to form a Wheatstone bridge structure by etching part of the SOI silicon film. The noise and signal-to-noise ratio of the output signal are compared to demonstrate the correctness of the simulation theory analysis, and the relationship between the sensor noise, signal-to-noise ratio and their structure is obtained. The research results of this paper have some reference value for the structural design of piezoresistive piezotransducers with high signal-to-noise ratio.
Structure design and simulation of MEMS sensor
1.1 Structure design of MEMS sensor
The structure of MEMS piezoresistive pressure sensor proposed in this paper is shown in Figure 1. In order to improve the sensitivity of sensor, SOI silicon wafer is used to make a raised sensor varistor structure. The sensor has a variety of varistor structures with different resistance lengths l and folded bars n, such as U, N, W, and VW. Figure 1 shows the sensor composed of a single varistor. The raised varistors R1 and R2, R3 and R4 are symmetrical in pairs, forming a Wheatstone bridge. The aluminum disks in relative positions are both input or output ends.

FIG. 1 Structure of MEMS silicon piezoresistive pressure sensor
The resistance value of varistor changes under the action of stress. The resistivity change caused by strain effect is much smaller than that caused by piezoresistive effect, and its resistance change rate can be approximately expressed as

Where: R is the initial resistance; ΔR is the variation of resistance value under stress. ρ is electrical resistivity; Δρ is the change of resistivity; π is piezoresistive coefficient; σ is stress.
The doping concentration of P-type varistor in this paper is 1017 cm-3, and the corresponding resistivity is about 0.202 Ω·cm.
Because the shear tangential stress on the piezoresistance bar is very small on the strain film with μm thickness, equation (1) can be reduced to
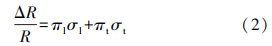
Where: πl and πt are longitudinal and transverse piezoresistive coefficients, πl = 73.5 × 10-11 Pa-1, πt = -67. 8 × 10-11 Pa-1; σl and σt are corresponding longitudinal and transverse stresses.
Under ideal conditions, the change rates of the initial resistance values of all resistors and the resistance values of symmetric positions are equal, R1 = R2 = R3 = R4 = R, ΔR1 = ΔR2, ΔR3 = ΔR4. The aluminum disks in the lower left corner and upper right corner are the input terminals, and the aluminum disks in the upper left corner and lower right corner are the output terminals. The output voltage Vout can be expressed as

In the formula, σR1x, σR1y, σR3x, and σR3y are the stresses of resistance R1 and R3 in the x and y directions in Figure 1, respectively. In order to ensure the linearity and sensitivity of the sensor output signal, it is necessary to select the appropriate film thickness. Too thick a film will reduce sensitivity, too thin will reduce linearity and load resistance. Considering the level of processing technology, the film thickness h was selected as 20μm in this paper. Within the full scale range of 0 ~ 300kPa, the sensor diaphragm side length a and thickness h should meet the following formula:

Where, P is the external pressure; E is the elastic modulus of silicon, E = 170 GPa; v is Poisson's ratio, v = 0.278.
According to Formula (4), the length of the elastic square sensitive diaphragm is less than or equal to 1184μm, and the diaphragm side length selected in this paper is 900μm. In this paper, the sensor uses SOI silicon interlinings with a thickness of 650μm. According to the wet etching Angle of 57.74°, the size of C-type silicon cup window is calculated to be 1172μm, and the size of the selected sensor chip is 3000μm×3000μm.
1.2 Finite element modeling and simulation analysis
In order to study the feasibility and output changes of each structure design, ANSYS finite element analysis software was used to model and simulate the MEMS piezoresistive pressure sensor of each structure. In this paper, the varistor material is borosilicate doped, the thickness is 4.5μm, and the surface is covered with a protective layer of silica 1μm thick. The structure of the varistor is followed by a 1μm insulating silica layer and a 20μm strain film. The bottom layer is a silicon cup, and the bottom of the silicon cup is bonded with the glass substrate through an anode.
FIG. 2 shows the strain of the thin film under applied pressure of 100kPa without resistance. σx and σy are the stresses in the x and y directions, respectively. FIG. 2 shows that the stress is greatest in the center of the edge of the strained film, so the varistor is generally placed there first. FIG. 3 shows the stress distribution after the introduction of a single type resistance with length of 50μm.

FIG. 2 Film stress distribution
According to the stress distribution in FIG. 2 and FIG. 3, varistor structures with different lengths l and folds n were designed and simulated successively. l and n grew from the center of the edge to the center and sides of the film. Combined with Formula (3), the simulation fitting relationship curve between sensor output and resistance structure n and l under 100 kPa and 6V input is obtained, as shown in Figure 4. As can be seen from Figure 4, Vout and sensor structure

FIG. 3 Stress distribution after resistance introduction
With the increase of l, the maximum value appears at about 75 μm. When l is long enough, Vout increases with n.

FIG. 4 Relation between Vout and n and l
2 Analysis of sensor noise and signal-to-noise ratio
2.1 Sensor noise analysis
The composition of pressure sensor noise is complex, mainly composed of thermal noise and scintillation noise. The total power spectral density of noise can be regarded as the sum of the spectral density of each noise power rate:

Where, VJ2 and Vf2 are the power spectral densities of thermal noise and scintillation noise respectively.
Thermal noise, also known as resistance noise, is generated by random motion of electric load current in varistor, and its form is similar to white noise. The power spectrum density of thermal noise is related to temperature, not frequency of voltage applied to resistance. Its expression is

Where: Boltzmann constant K = 1.38× 10-23 J/K; Temperature T = 300 K; R is the value of resistance; ρ is electrical resistivity; w is the resistance width, w = 10 μm; t is the resistance thickness, t = 4.5 μm.
Scintillation noise is caused by the slow fluctuation of emitting electrons caused by the local fluctuation of the device. Its power spectral density is inversely proportional to the frequency and usually appears in the low frequency range. The calculation formula is

Where: q is the doping concentration, q = 1017cm-3; Vin is the input voltage; N is the number of carrier; f is the noise frequency; a is the Hooge factor, which is the parameter related to the sensor manufacturing process, usually 10-7 < a < 10-3. According to the sensor material and doping concentration, 10-5 is used in this paper.
According to equations (5), (6) and (7), the relationship between the noise power spectral density V2 noise and frequency f is obtained under different conditions of constant voltage input of 6V, l of 50μm and n, as shown in FIG. 5. And the correlation between noise power spectral density V2noise and varistor structure n and l at 6V constant voltage input and 1Hz, as shown in Figure 6.

Figure 5V2 noise in relation to f

FIG. 6 Relation between V2 noise and n and l at 1Hz
From FIG. 5 and FIG. 6, it can be seen that sensors of various structures are mainly affected by scintillation noise. The low frequency range is dominated by scintillation noise, and only in the high frequency part will thermal noise gradually become the main component of noise, and the amplitude is very small. At the same low noise frequency point, the noise power spectral density decreases with the increase of n and l.
2.2 Sensor signal-to-noise ratio analysis
The total circuit noise is the sum of the noise power spectral density in the measurement frequency band. Through equations (3) and (5), the signal-to-noise ratio SNR, namely Vout/Vnoise, can be expressed as

Where, fmax and fmin are the upper and lower cut-off frequencies of noise respectively.
Figure 7 shows the relationship between SNR, n and l of the sensor at 6V input and 1-30Hz bandwidth. As can be seen from Figure 7, the signal-to-noise ratio is affected by the chip structure and increases with the increase of n, first rises and then falls with the increase of l, and the optimal resistance length is generally about 125μm.

FIG. 7 Relation between SNR and n and l
3. Experimental results and analysis
3.1 Sensor preparation
In this paper, the standard MEMS technology is used to make the sensor chip. The production process mainly includes the following steps: cleaning the SOI silicon wafer, ion implantation, thermal oxidation to form a protective layer, photolithography etching varistor, contact hole, sputtering aluminum, photolithography etching aluminum, bottom silicon cup window, corrosion silicon cup, removal of bottom protective layer, anode bonding glass substrate.
The sensor chip prepared by the above process is shown in Figure 8. In this paper, three single chips with lengths of 50, 100 and 150μm were prepared. The length of the multi-strip chip is fixed at 50μm, and the number of folded strips is 2,3,4, and 6. Figure 9 shows the real picture of one sensor after welding gold wire and packaging.
3.2 Pressure measurement and calibration.
The calibration test platform is shown in Figure 10. PLATINUM vacuum pump and const162 table pump are used to generate pressure loads of 0 ~ 100 kPa and 100 ~ 300kPa, respectively. At room temperature of 27 ℃, sample points of pressure load with a step of 30 kPa were selected in the pressure range of 0 ~ 300 kPa. The output characteristics were tested as shown in FIG. 11. FIG. 11 (a) shows the relationship between output signals of different varistors and pressure, FIG. 11 (b) shows l = 50 μm. n Different varistor output signals and pressure relationship. As can be seen from Figure 11, the sensor works well and has a high linearity within the range of 0 ~ 300 kPa.

Figure 8. MEMS Piezoresistive pressure sensor chip

FIG. 10 Calibration test platform
3.3 Sensor noise measurement
Keep the temperature unchanged, in the standard atmospheric pressure constant voltage source input, output signal Vout there is noise from many aspects, such as the power supply noise, the noise of the sensor itself, the noise of the test instrument, the noise of the external environment. In order to eliminate the input power supply noise, the battery is used as the power supply; In order to reduce the noise of the test instrument, the phase-locked amplifier in HB-521 weak signal detection device is used in this experiment. In order to shield the interference of external electromagnetic fields, metal shielding boxes are used, and coaxial cables are used to connect the devices. The experimental device is shown in Figure 12.
The output signal of the sensor, Vout, was connected to the HB-521 phase-locked amplifier for amplification. The center frequency of the phase-locked amplifier was set at 15Hz and the time constant at 10 ms. A U-shaped pressure sensor with length of 50 μm is used to input 3, 6, 9, 12 V voltages under standard atmospheric pressure. The amplitude-frequency curve of the measured noise voltage Vnoise is shown in FIG. 13.

Figure 11 Vout output curve


The total noise measured by the phase-locked amplifier includes sensor noise, amplifier noise and power noise, and its relationship can be expressed as
Where, Vsum, Vsensor, Vamp and Vpower are total noise, sensor noise, amplifier noise and power noise respectively.
In the aspect of power supply, the battery with low noise is used as the power supply, and the noise of the amplifier can be ignored. The noise of the amplifier can be obtained by directly measuring the small resistance of the lock amplifier.
The relationship between noise voltage Vnoise and l, n and Vin is shown in Figure 14.

(a) Input 3 V Vnoise amplitude-frequency curve

(b) Input 6 V Vnoise amplitude-frequency curve

(c) Input 9 V, Vnoise amplitude frequency curve

(d) Input 12 V, Vnoise amplitude frequency curve
Figure 13 Vnoise amplitude-frequency curve

(a) n = 1, l = 50, 100, 150 μm

(b) n = 1, 2, 3, 4, 6, l = 50 μm
Figure 14 Relationship between Vnoise and Vin
It is found that scintillation noise is the main noise source in low frequency band, which is proportional to Vin. When the Vin is too low, for example, when the input voltage is 3 V, the measurement error of Vnoise will be large due to the impact of the amplifier noise. When the Vin is large, the noise measurement result is more accurate. It can be seen from Figure 14 that Vnoise is proportional to Vin as a whole, and Vnoise decreases with the increase of n and l.
According to the measured Vnoise, Vout and Equation (8), the relationship between the signal-to-noise ratio and the resistance structure can be obtained, as shown in Figure 15. As can be seen from the figure, SNR does not change with Vin. When Vin is low, the Vnoise is difficult to be accurately measured, and the deviation of SNR is large. The difference between the experimental SNR and the theoretical value is within 20%, and there is a good agreement between the measured SNR and the theoretical value, which proves the reliability of the theoretical analysis.
4 Conclusion
In this paper, the MEMS pressure sensor based on signal-to-noise ratio is designed and analyzed. Firstly, the stress distribution of each structure transducer is simulated by ANSYS finite element method. Secondly, MEMS technology is used to design and manufacture part of the sensor chip, and processing package; Then the pressure generator is used to calibrate the sensor. Finally, different voltages were input to explore the relationship between noise, signal-to-noise ratio and pressure-sensitive structure of MEMS piezoresistive pressure sensor. The following conclusions can be drawn:
(1) Through simulation, it is found that pressure sensitive structure of sensor has influence on noise, output signal and signal-to-noise ratio. Increasing the number of varistor folds is usually helpful to obtain lower noise and higher output signal and signal-to-noise ratio. The optimal resistance lengths based on output signal and signal-to-noise ratio are about 75 μm and 125 μm, respectively.
(2) The experiment verifies that the noise is proportional to the input voltage, and the Vnoise decreases with the increase of n and l, while the SNR does not change with the change of the input voltage. SNR is mainly related to the sensor structure, which proves the correctness of the theoretical analysis. The research results of this paper have a certain reference value for improving the signal-to-noise ratio of sensors and developing high-precision sensors.
References:
[1] Hao Xuhuan, Chang Bo, Hao Xuli. Development Status and Application of MEMS Sensors [J]. Wireless Internet Technology, 2016 (3) : 95-96.
[2] Wang Yin, Zhang Jiahong, Li Min, et al. Design, Fabrication and Performance Compensation of a New Silicon Piezoresistive Pressure Sensor [J]. Electronic Devices, 2019,42 (6) : 1371-1377. (in Chinese)
[3] Wu Peishan, Liu Qin, Li Xin, et al. High Temperature Piezoresistive Pressure Sensor of monocrystalline Silicon [J]. Instrument Technology and Sensor, 2020 (10) : 1-3.
[4] Hao Jianhong, Fan Zonghao, Li Yi. Research and Design of an Improved beam-Island-membrane Pressure Sensor [J]. Instrument Technology and Sensor, 2019 (4) : 10-14.
[6] ZARNIK M S, BELAVIC D, SEDLAKOVA V, et al.Com parison of the intrinsic characteristics of LTCC and silicon pressure sensors by means of 1 / f noise measurements [J]. Radioengineer⁃ ing, 2013,22 (1) : 227-232.
[7] BAE B, FLACHSBART B R, PARK K, et al. Design optimi⁃ zation of a piezoresistive pressure sensor considering the out⁃ put signal⁃to⁃noise ratio. Et al. Design optimi⁃ zation of a piezoresistive pressure sensor considering the out⁃ put signal⁃to⁃noise ratio. Journal of Micromechanics & Microengineering, 2004,14 (12) : 1597-1607. Research on Design, Manufacture and Test of MEMS Pressure Transducer with Silica-Al Heterogeneous Structure [J]. Chinese Journal of Sensors and Actuators, 2018,31 (7) : 998-1004.
[9] ZHANG J H, CHEN J X, LI M, et al. Design, fabrication, and im⁃ plementation of an array⁃type MEMS piezoresistive intelligent pressure sensor system [J]. Micromachines, 2018, 9:104.
[10] Wang Weizhong, He Hongtao, Bian Yumin, et al. A MEMS High Temperature Pressure Sensor [J]. Microelectronics, 2016,53 (6) : 387-393. (in Chinese)
[11] Du Zhi, He Jianbo. Design of Resistive Pressure Sensor Based on MEMS [J]. Instrument Technology and Sensor, 2019 (6) : 19-22.



