Temperature compensation of pressure sensor based on hybrid optimization algorithm
Piezoresistive pressure sensor is widely used in various fields, but piezoresistive pressure sensor has the disadvantage of temperature drift. Because its measurement accuracy is greatly affected by temperature, it can not be used in the large range of temperature difference, which restricts the development of the practical process of piezoresistive pressure sensor, so it must be temperature compensation for piezoresistive pressure sensor. Eliminate its sensitivity to temperature.
Experts and scholars have conducted in-depth research on the temperature compensation method of sensors. In literature, BP neural network is used to establish the temperature compensation model, and particle swarm optimization algorithm is used to optimize the BP neural network, so as to avoid the BP neural network falling into the local minimum and improve the complement. In literature [5], RBF neural network was used to establish temperature complement, and ant colony optimization algorithm was used to optimize R-BF neural network to improve compensation accuracy. In literature [6], genetic simulated annealing algorithm was used to establish the temperature compensation model. The improved hardware circuit proposed in the literature uses M A X 1452 signal conditioning chip to compensate the temperature of the pressure sensor. The experiment shows that this compensation circuit has a good compensation effect. Compared with the compensation method of software method, the implementation process of this method is relatively complicated, and it is not easy to transplant other types of sensors.
Working principle of pressure sensor and temperature compensation principle
The influence of temperature on the pressure sensor is mainly reflected in that the piezoresistive coefficient is a function related to temperature. The piezoresistive coefficient will decrease with the increase of temperature and increase with the decrease of temperature. Secondly, when the ambient temperature changes, additional thermal stress will be generated on the sensor. Because the diffusion resistance has different coefficient of thermal expansion, the accessory piezoresistive effect will be generated.
Figure 1 Working principle of piezoresistive pressure sensor
1.2 Principle of temperature compensation
The principle of temperature compensation for the sensor is shown in FIG. 2. Generally, the pressure sensor is greatly affected by temperature in the low and high temperature segments, so the compensation performance is better at this stage. However, the RBF neural network model with high system requirements is used for compensation, and the ordinary linear least square compensation model can be used in the middle segment. The switch between different compensation models is realized by setting the temperature threshold.
2. Linear least square compensation model
The linear equation is used to compensate the temperature of the sensor:

Where, O/is a constant term; Is the coefficient; e is the fitting error. It can be known from literature [10] that:
When using the linear fitting equation for fitting, in order to make the linear fitting interval as large as possible, so as to improve the efficiency of the overall temperature compensation method and reduce the computational complexity, it is necessary to automatically search the interval of the intermediate linear segment according to the accuracy requirements. Let the initial interval be [t, t: ] = [t0, t], carry out linear fitting to the initial interval, and obtain the maximum fitting error emax. If it is greater than the lower limit of error, set t1=t + π, where is the sampling interval of temperature value. Carry out linear fitting to the newly generated interval again, and obtain the maximum fitting error e if it is still greater than the lower limit of error. Then let t2=t: 1. Carry out linear fitting for the newly generated interval again, and repeat the cycle until the maximum value of fitting error e is lower than or equal to the lower limit of error n.
3. RBF neural network temperature compensation model
3.1 RBF neural network
RBF neural network is usually composed of input layer, hidden layer and output layer, hidden layer output is:
Where, is the width of the basis function; C is the implied node center. The output layer is:
Where, W is the connection weight of the hidden node and the output node; b0 is the output deviation.
In RBF neural network, the width of the basis function, the central Ci of the hidden node and the connection weight Wi of the hidden node and the output node are the basic parameters that need to be determined.
In order to improve the generalization ability of conventional RBF neural network, this paper adopts hybrid optimization algorithm to obtain the width of the basis function of the optimal RBF neural network, the center G of the hidden node and the connection weight value of the output node, and gives full play to the excellent global search ability of the evolutionary algorithm and the excellent local search ability of the gradient descent algorithm, so as to improve the temperature compensation effect of the nonlinear segment of the sensor. The specific methods are as follows:
Firstly, basic parameters such as population size, number of elite individuals and operation probability should be set in the hybrid optimization algorithm.
Then, binary coding is adopted to encode the nodes of the hidden layer, and real coding is adopted to encode the width of the basis function and the center C of the hidden node, such as mixed coding. The structure of mixed coding is shown in Figure 3.

Figure 3 Hybrid coding structure
After that, the training samples are used to train the neural network. If the termination conditions are met, the optimization will be stopped, and the parameters involved are the optimal network parameters, and the temperature compensation model is established.
If the termination condition is not met, the weighted fitness function is used to calculate the individual fitness value. When the conventional R, B and F neural network is optimized by evolutionary algorithm, the fitness function used is the error of training sample. The over-fitting phenomenon brought by this approach will lead to a small error in training, but still a large error in testing. One way to solve the problem is to use weighted error congruence as a fitness function:
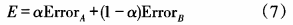
Then, in order to improve the local search ability of the algorithm, the gradient descent algorithm is used for the iterative search of elite individuals in the new evolved population, and the probability is P. For individuals without gradient descent algorithm, simplex crossover operation and uniform mutation operation are carried out. The simplex crossover operation can make the optimization algorithm have good global optimization ability and local optimization ability respectively in the early and late evolutionary stage. The uniform mutation operation can improve the diversity of population and avoid the precocious phenomenon.
Finally, continue to use training samples to train the neural network, and cycle the above optimization process until the termination condition is met.
4 Experimental Research
The temperature compensation method of pressure sensor based on hybrid optimization algorithm is verified experimentally. The pressure sensor is placed in a temperature environment of 20 ℃ ~ 80 ℃, and the temperature changes by 10 degrees each time, and the constant temperature environment is guaranteed. 5kPa and 55 kPa pressure are applied to the sensor respectively, and each change is 5kPa. The measured value of the calibrated sensor pressure value at different temperatures is compared with the actual pressure value to obtain the measurement error, and the error is plotted as a curve, as shown in Figure 4.
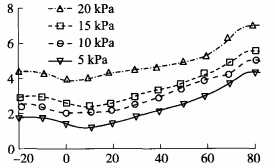
It can be seen that the sensor error changes nonlinear in the low temperature range of -20 ℃~ 10 ℃ and the high temperature range of 55℃ ~80 ℃, while the sensor error changes linearly in the temperature range of 1O℃~ 55℃. Therefore, linear least square method was used for fitting within the temperature range of 10 ℃ ~ 55 ℃, and hybrid optimization RBF neural network temperature compensation model was used at both ends. Parameters were set as shown in Table 1.
Conventional RBF neural network and hybrid optimized neural network were used for comparative study.
After 100 training iterations, the training accuracy of hybrid optimized R BF neural network reaches 1.121x 10-4, while that of conventional R BF neural network is 1.657 ×10-2. It can be seen that the hybrid optimized RBF neural network has higher training accuracy and efficiency than the conventional RBF neural network.
Four methods are used to compensate the temperature of the pressure sensor in the range of 5kPa ~ 55kPa pressure and -2O ℃ ~ 80 ℃ temperature:
The data corresponding to each temperature value in Table 2 are the average error values at each pressure point of 5kPa ~ 55kPa when this temperature compensation method is used. In the range of 20 ℃ ~ 80 ℃, the average error of temperature compensation method 1 is 1.92 %, the average error of temperature compensation method 2 is 1.09%, the average error of temperature compensation method 3 is 0.55%, and the average error of temperature compensation method 4 is 0.5.3 %.
The linear least squares temperature compensation model is used in the temperature range of -20 ℃ ~ 80 ℃. The linear least squares temperature compensation model shows a better compensation effect in the temperature range of 10 ℃ ~ 55 cC, and the error is less than 1%. However, in the low temperature and high-end area at both ends, the error is larger, ranging from 2% to 3%.
The conventional RBF neural network temperature compensation model is used in the temperature range of -20 ℃ ~ 80 ℃, showing a better fitting effect of the RBF neural network temperature compensation model, and the error is controlled about 1%.
The hybrid optimization RBF neural network temperature compensation model is used in the temperature range of -20 ℃ ~80 ℃, showing the optimization performance of the hybrid optimization algorithm used in this paper on the RBF neural network temperature compensation model, and the error is controlled within l %.
The linear least square temperature is used in the temperature range from l0℃ to 55 ℃
In the degree compensation model, when the temperature is -2O ℃~ 10℃ and 55 ℃~ 80 ℃, the hybrid optimization RBF neural network temperature compensation model is used, and the error is controlled about 0.5%, which is not much different from method 3, but the temperature compensation speed is greatly improved in the temperature of 10℃ ~ 55 ℃, and the overall temperature compensation efficiency is improved.
5 Conclusion
① When the linear least square temperature compensation model is used in all temperature ranges, the compensation effect is better in the intermediate temperature range, but the error is larger in the low temperature and high-end area at both ends.
② When the RBF neural network temperature compensation model is used in all temperature ranges, the better fitting effect of the RBF neural network temperature compensation model is shown.
③ The hybrid optimization algorithm was used to optimize the RBF neural network temperature compensation model, which improved the compensation effect.
(4) Using the linear least square temperature compensation model in the middle temperature range, using the hybrid optimization RBF neural network temperature compensation model in the low temperature and high-end areas at both ends, can greatly reduce the influence of temperature on the sensor, and improve the overall temperature compensation efficiency.



