Research on high precision pressure sensor compensation method in wide temperature region
Silicon piezoresistive pressure sensor has the advantages of high sensitivity, fast dynamic response, good stability and wide operating temperature range. It is widely used in aviation, aerospace, ships and other fields [1]. Pressure monitoring in some key parts of aircraft, weapons and ships, such as rocket propellant storage tank [2]. Its measurement accuracy directly affects the overall performance. At present, silicon piezoresistive pressure sensors generally have large temperature drift. Therefore, the temperature compensation method of silicon piezoresistive sensor is studied to improve the measuring accuracy. Because of the material properties of silicon, the temperature change will cause the change of the varistor and piezoresistive characteristics. As a result, large zero drift and sensitivity drift [3] are caused, leading to the increase of the total error of the sensor in the working temperature range, so it is necessary to carry out temperature compensation. Currently, the commonly used compensation methods include hardware compensation and software compensation. The hardware compensation circuit is complicated and difficult to debug. It is not suitable for engineering [4], and software compensation generally has surface fitting [5]. Spline interpolation and neural network algorithm [8]. It has a good effect on improving the accuracy, but the surface fitting and neural network algorithm require a lot of computation. To the MCU implementation caused greater difficulty. However, a single spline interpolation algorithm requires more interpolation points. To increase the complexity of application operation, this paper based on the original output characteristics of the silicon piezoresistive core. A method combining acquisition circuit, curve fitting and cubic spline interpolation algorithm is proposed, and experimental verification is carried out. The method improves the measurement accuracy of sensor, has engineering operability, and can be applied to the field of pressure sensor in aviation, aerospace, ships, etc.
1 core voltage acquisition circuit
Since the sensitivity of silicon piezoresistive core is generally ten to dozens of mV/V, when the bridge supply voltage is 3 V, its output voltage is generally not more than 50 mV. To achieve the measurement accuracy of a few 10,000, the acquisition circuit is required to be high.
Encapsulating the pressure-sensitive bridge and the temperature-measuring platinum resistance in the pressure-sensitive core can more accurately measure the ambient temperature of the pressure-sensitive bridge and improve the compensation accuracy. Compared with directly sputtering the platinum resistance on the sensitive core [9]. Compared with the warm/pressure composite core scheme, the temperature coefficient of the pressure sensitive core needs to be extracted [10]. The more simple remote pressure sensitive bridge is powered by A precise reference source, and its output enters A 24-bit A/D through a differential amplifier circuit. Differential amplifying circuit can effectively suppress common-mode noise. The 24-bit A/D selected in this paper has 20 significant bits when the sampling rate is 10 Hz. When the reference voltage is 3V. The voltage measurement accuracy is 0.002mV, which can meet the measurement requirements. The demodulation of the remote platinum resistance also passes through the bridge, the differential circuit enters the 24-bit A/D, and the A/D conversion result is output to the single chip microcomputer, which divides the amplified voltage by the amplification factor to obtain the original voltage of the two Bridges. The single chip microcomputer performs the acquisition task. Calibration program and compensation algorithm, the final conversion result output to the top machine remote.
2 core original data acquisition
Put the 2.5MPa pressure sensor into a high precision temperature chamber. The temperature point is set and the high precision pressure gauge is used for loading. The original output voltage of the measured pressure-sensitive bridge and temperature bridge is shown in Table 1.
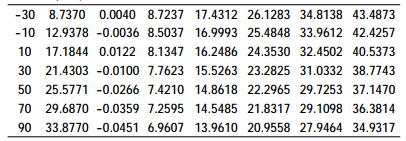
Table 1 Original output of pressure-sensitive bridge and temperature bridge at different temperatures
Output data of pressure-sensitive bridge at different temperatures are drawn into curves, as shown in Figure 2.
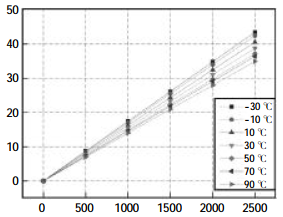
FIG. 2 Output of pressure-sensitive bridge at different temperatures
As can be seen from FIG. 2, at constant temperature, the loading pressure and the bridge output voltage present a good linearity, which can be obtained with multiple terms fitting with high precision and small amount of computation, thus saving SCM resources. The sensitivity of pressure sensitive core has obvious drift between different temperatures. The sensitivity of temperature distance varies from one to another, so the appropriate fitting method should be selected according to the curve of sensitivity changing with temperature.
3 Compensation algorithm
Set a constant temperature Tj, apply pressure Pi to the sensor, and read the output value of the corresponding pressure core Vi, i= 1,2, N, that is, there are N groups of readings at Tj, I, V1, P2, V2, PN, VN, where N=6, that is, 6 pressure loading values.
The least square method was used to fit the polynomial calibration curve at temperature Tj.
According to the data in Table 1, the least square fitting method was used to calculate the polynomial coefficients at different temperatures, as shown in Table 2. The temperature bridge voltage and coefficient were plotted as curves, as shown in Figure 3.
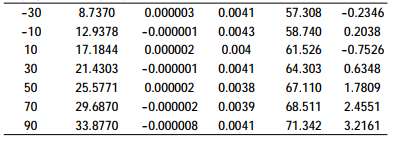
Table 2 Fitting coefficients at different temperatures
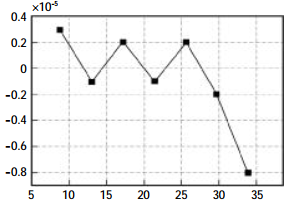
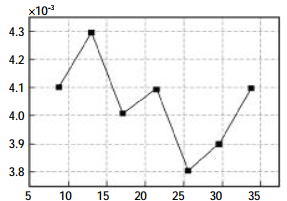
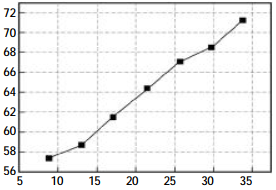
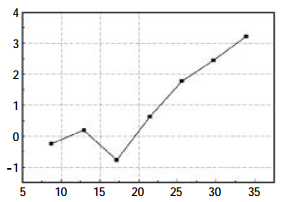
FIG. 3 Relation between temperature bridge voltage and coefficient
As can be seen from the figure above. The linearity of temperature bridge and various coefficients is very poor. If the least square polynomial fitting is adopted, it will bring a large error when the number of terms is small, and the calculation amount of single chip microcomputer will be greatly increased when the number of terms is large. In view of this, cubic interpolation algorithm is adopted to carry out curve fitting for the relationship between temperature bridge voltage and various coefficients. The first and second derivatives also have continuity, which is widely used in engineering [11]
Each polynomial coefficient C0~C3 is composed of 6 cubic polynomials. The specific form is as follows.
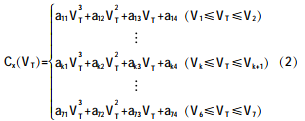
The temperature bridge voltage collected by single chip microcomputer can be solved by cubic spline interpolation to obtain the coefficients of any temperature point, through the coefficients and the collected pressure bridge voltage, the least square curve fitting to obtain the pressure value.
4 Test
The algorithm and the original data are written into the single chip microcomputer, which calculates the collected data in real time and directly obtains the pressure value. In order to verify the effectiveness of the algorithm, the pressure sensor is again placed in a high-precision temperature box, the temperature point is set, and the high-precision pressure gauge is used for loading. Under different temperatures and loading pressures, the output pressure of the single chip microcomputer is shown in Table 3, and the full-scale error of each measuring point is shown in Figure 4.
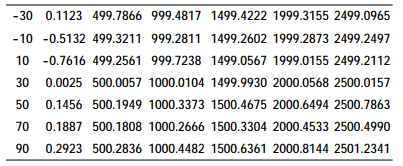
Table 3 Output pressure of sensors at different temperatures
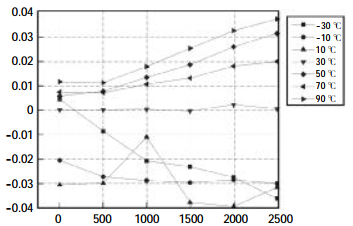
FIG. 4 Measurement errors of pressure sensors at different temperatures
As can be seen from Table 3 and Figure 4, the single chip microcomputer can accurately output the measured pressure value after temperature compensation. After temperature compensation, the pressure sensor has a high measurement accuracy, ranging from -30 to 90, and the measurement error of the sensor is within 0.04%FS in the temperature range.
5 Conclusion
In this paper, the high precision acquisition circuit based on single chip microcomputer is adopted to improve the original voltage measurement accuracy of the pressure-sensitive core and the temperature bridge. At constant temperature, the loading pressure and the output voltage of the pressure-sensitive core present good linearity. The least square fitting method can reduce the amount of calculation. Thus using cubic spline interpolation, in order to reduce the error of remote, the two algorithms combined use, after the temperature compensation of the pressure sensor has a high measurement accuracy, in -30~90 degrees, the temperature range of the sensor measurement error is within 0.04FS, the circuit and algorithm is simple and easy to operate.
Institute of reference literature
[1] Liang Zengshou. Recent development and application of Silicon Piezoresistive Pressure Sensor [J]. Piezoelectrics and Acoustooptics Yuan 1983, 5, 1, 15-20.
[2] Wei Yanming, Yuan Songtao, Liang Junqiang. Space Control Technology and Applications, 2010, 36, 4, 25-30.
[3] Lee Y T, Seo H D, Kawamura A, et al.Compensation method ofoffset and its temperature drift in silicon piezoresistive pressuresensor using double wheatstone - bridge configuration [C]//International Conference on Solid - state Sensors & Actuators.IEEE Yuan 1995 Yuan 570-573.
[4] Liu Ye, Zhang Lu, Yang Xinwei, et al. Research on zero temperature drift Compensation of Pressure Sensor Using Hardware Neural Circuit [J]. Journal of Xi 'an Jiaotong University, 2010, 44, 8, 10-14.
[5] Zeng Mingru, Liu Liang, Qian Xin, et al. Surface Fitting Compensation of diffused Silicon Pressure Transmitter [J]. Science Edition of Nanchang University, 2011, 35, 1, 43-46.
[6] Wang Bingbing, Li Huaijiang. Temperature Compensation of Silicon Piezoresistive Pressure Sensor Based on Cubic Spline Interpolation [J]. Chinese Journal of Sensors and Sensors, 2015, 28, 7, 1003-1007.
[7] Wang Pitao, Zhai Diantang, Cheng Xie Feng. Pressure Sensor Temperature Compensation Based on Cubic B-spline Interpolation [J]. Information Technology and Informatization Yuan 2007, 32, 3, 112-113+115.
[8] Xia Xiulan, Zhao Li. Research on Multi-sensor Information Fusion Based on BP Neural Network [J]. Computer Measurement and Control, 2015, 23, 5, 1823-1826.
[9] Zhang Ting, Li Hongzhi, Yuan Lanhui, et al. Research on Temperature Characteristics and Compensation Algorithm of high precision Marine Pressure Sensor [J]. Journal of Marine Technology, 2016, 35, 6, 36-40.
[10] Xie Feng, Yuan Chengwenjin, Cao Yongquan. Research and Design of high precision Temperature-pressure Composite Sensor Based on Data Processing [J]. Chinese Journal of Sensors and Actuators, 2017, 30, 12, 1845-1849.
[11] Li Xin, Qiao Aimin. Application of Cubic Spline Interpolation in Error Compensation of Weighing Instrument [J]. Electronic Design Engineering, 2011, 19, 11, 48-50.
[12] Yan Qingjin. Numerical Analysis [M]. Beijing Academy Beihang University Press, 2012.



